Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of
successes in draws without replacement from a finite population wherein each draw is a success or failure.
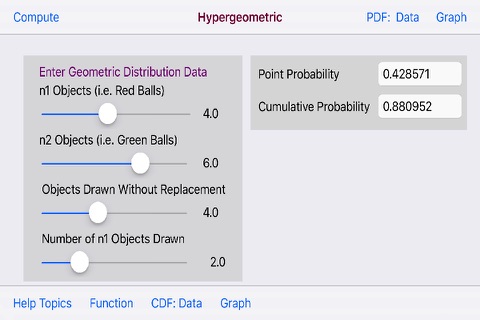
For Data Entry the Hypergeometric Distribution app utilizes four Sliders to enter 4 data variables. (1) the n1 variable ( i.e. number of red balls ) (2) the n2 variable ( i.e. number of green balls ) (3)
the n variable which the total sample size which is the addition of the n1 and n2 variables and (4) the k variable. For this app the k variable is number of n1 objects ( i.e red balls ) that are withdrawn with replacement to consider for the probability calculation.
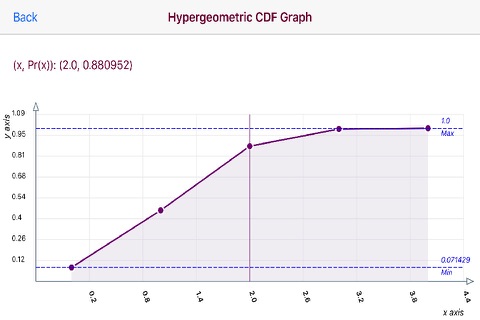
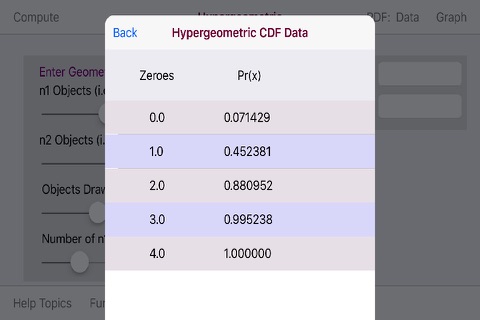
The Hypergeometric Distribution app has the graphing ability to graph the PDF and CDF distributions for the selected variables.
The graphs are touch enabled graphs. Upon touching the graph a vertical line appears. Move the vertical line to the left or right to display the point (x/Pr(x)) data in the upper left of the graph.
The horizontal x-axis displays x values. The vertical y-axis plots a range of Pr(x) values.
Horizontal Max and Min dashed lines display the Maximum and Minimum Pr(x) values
Since the Hypergeometric Distribution is a Discrete Probability Distribution a dot (.) indicator is utilized to display each discrete data pair.